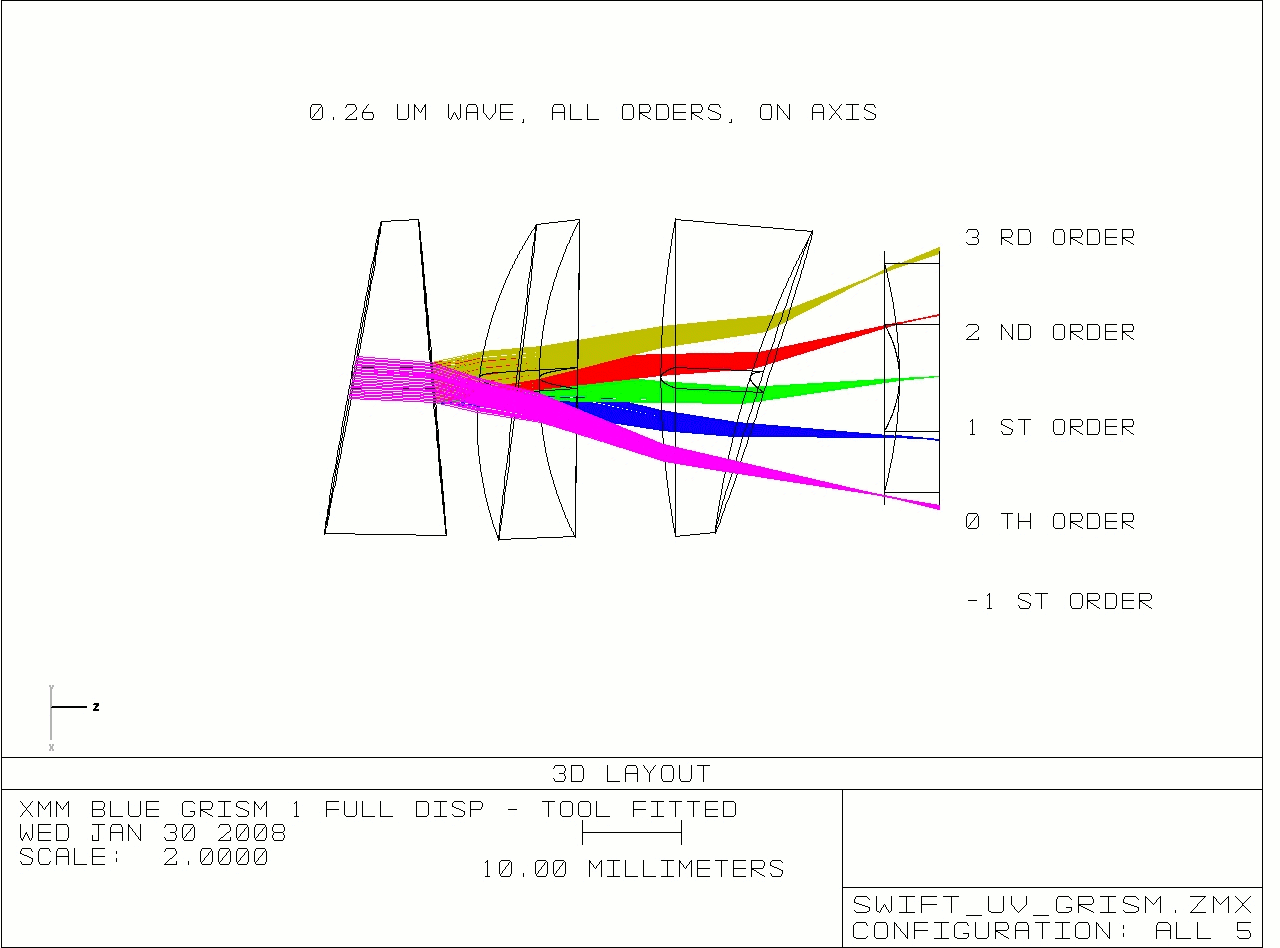Swift UVOT Calibration
report
Zemax optical models for the UV-Grism study:
Zemax pixel scale factor and positioning
Date:
2008/05/27
Version: 1.0
Prepared
by: N. Paul M. Kuin, (MSSL/UCL)
Relevant Documents
description Zemax program: TBD
description Zemax UVOT model: TBD
description Swift mission: Gehrels
et al. 2004.
description UVOT instrument:
Roming et al. 2005, see also the XMM-OM description: Mason et
al. 2001.
SWIFT-UVOT-CALDB: Swift
UVOT Grism Clocking, Alice Breeveld, 19th October 2005, Revision
#01, Swift UVOT Calibration Documents Version 06-Apr-2006
SWIFT-UVOT-CALDB: Teldef Files, Alice Breeveld, 19th October
2005, Revision #01, Swift UVOT Calibration Documents Version
06-Apr-2006
Introduction
The Swift UVOT grism calibration will be more reliable using the
knowledge of the Zemax model that was used to design the grisms for
the instrument. We establish in this report how valid the model is,
by making a simple comparison of the on-axis model result for the UV
grism, with an on-axis observation (the boresight of the instrument
should be the optical axis because of rotational symmetry).
The
original design model and the actual instrument show that the
mounting of the grisms was a few degrees rotated as is evident of the
angle of the dispersion on the detector. The correction, based on the
nominal and clocked angles of the grism spectra on the
detector, is 3.8 ± 0.2 degrees for the UV Grism. That is
the only correction made to the original zemax grism design model.
The original model was optimised for the 260nm wavelength in the
first order. In particular that means that the 260nm point in the
first order falls at the center of the predicted zemax image.
The
instrument boresight is know to vary slightly for the different
lenticular filters. The boresight of the grisms is not known.
Instead, a point in the zero order, for the boresight spectrum, which
we will refer to as the anchor point of that spectrum, was
adopted. The anchor point for any spectrum in the
current calibration is found where the zero order flux peaks,
with a possible correction to obtain a consistent aspect solution
over the image. Although this was a solution giving some kind
of reference point for each spectrum, it is not known which
wavelength range this corresponds to, nor how accurate it is.
Currently, (May 2008) the uvot software is basing its anchor points
on a fit of the zero order peaks of weak sources with orders between
5 and 10 pixels, to the USNO-B1 positions, after doing a distortion
correction. Obviously, the accuracy is better than 10 pixels, with an
estimated accuracy of about 3 pixels. Since the dispersion in
first order is about 3Å/pixel, that translates to an estimated
10Å uncertainty.
A major problem of that approach is,
that more than 20% of the first order spectra on the detector do not
have a corresponfing zero order, thus lacking a means to calibrate
their wavelength scale for which the anchor point is needed.
Considering that the detector was optimised in the design for the
first order, it is appropriate to study the grisms using the zemax
model, in order to determine a method for establishing the wavelength
scale in the first orders independently of the zero order, or,
perhaps, establish a prediction for the position of the missing zero
orders. Also, the zemax model can predict the dispersion of all
orders over the detector which is essential for these spectra, since
the second and third order fall generally on top of the longer
wavelengths in the first order. Moreover, the angle of the spectral
orders, and distortion should in first order come out of the zemax
model. Finally, the point spread function of incoming radiation as
function of wavelength, order and position is predicted by the model,
and will be useful for these are not nice gaussians, but rather
elongated donuts for the higher orders, as can be seen in Figure 2
below.
As a first step, we will determine the scale factor of
the zemax pixels using the predicted and observed dispersion at the
optical axis/boresight. Next we determine the shift needed from
the predicted zemax spectrum to the observed spectrum by
fitting the 260nm spectral feature and the zemax 260nm point using a
shift in X and Y.
A good fit will prove that the zemax
model is useful for the calibration of the grisms.
Overview of the Zemax optical model for the Swift UVOT grisms
Zemax is a computer program using ray-tracing techniques to model
optical systems (see http://www.zemax.com). Zemax works with an
optical model of the system (i.e., the UVOT telescope + grism or
filter ) whereby the geometric properties of all elements are
specified, see Figure 1. The UVOT model of the UV grism, for example,
has a grism glass specification which is valid upwards of 200nm, and
which for the current study has been extended with a linear
approximation to shorter wavelengths.
Zemax has optimization
options, where chosen elements of the optical train will be adjusted
to find the best solution to obtain a certain result in the image
plain, like a shift of the image of a source along the optical axis.
We do not make any such adjustments to the original Zemax optical
model used for the Swift UVOT (and XMM OM) design. The
input for each ray computed is the field position of the incident ray
(expressed as the angles in X and Y from the optical axis), and the
wavelength of the incident ray. Since at each optical surface there
is a small uncertainty in the resulting geometry, caused by, for
example, surface roughness, the ray can calculated many times,
randomising and propagating these uncertainties. This then results in
a spot image, which is representative of the PSF of the system. In
the image plane the resulting image can be built up, see Figure 2.
In the current study only the center point was calculated for each
ray.
|
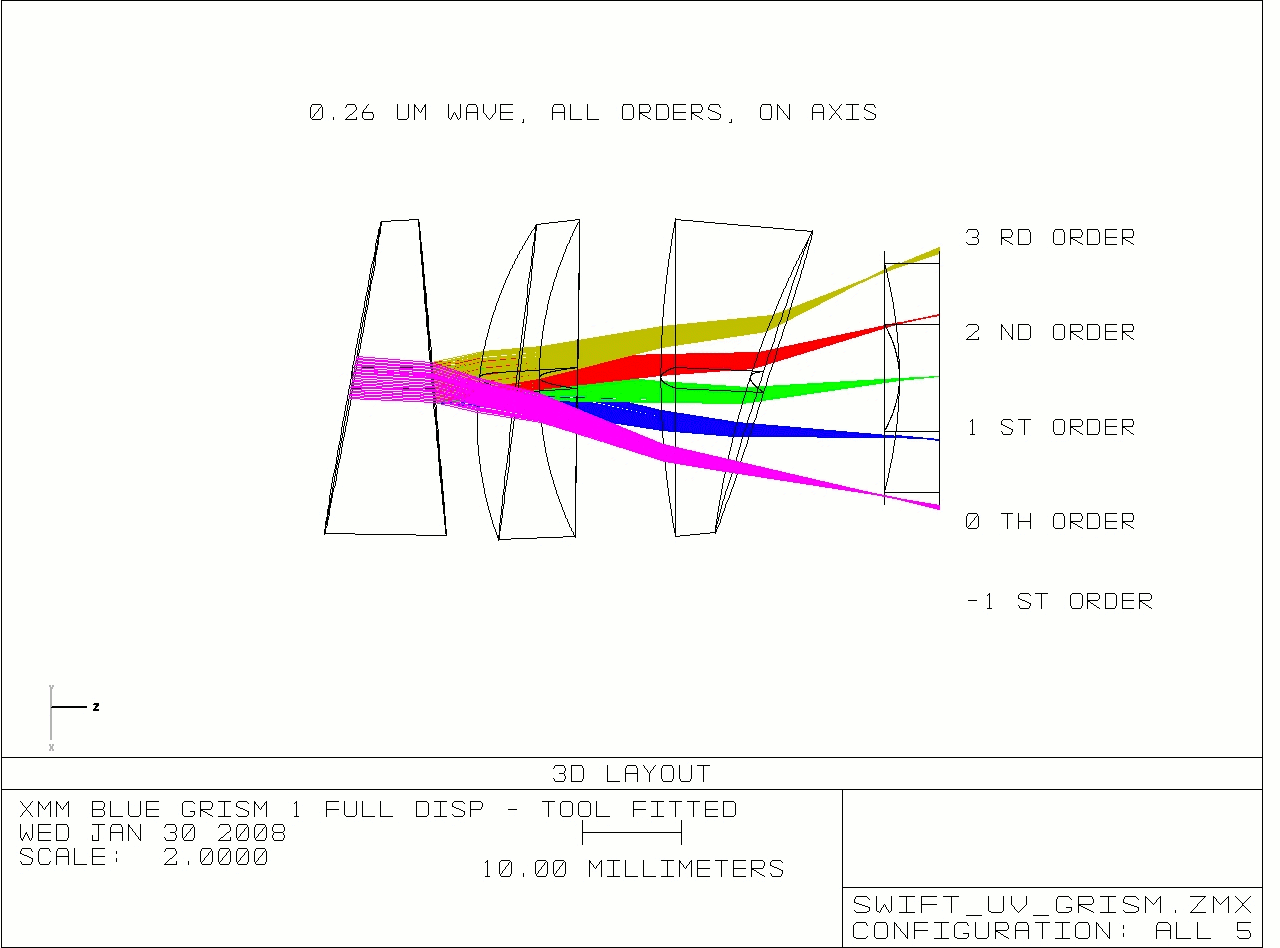
|
|
Figure 1: Sideway view of the grism section of the
UVOT Zemax model. The telescope secion in front has not been
included here, but is in the model. Incoming rays are on-axis from
the left. Different spectral orders are colour coded. Five orders
are displayed, with the minus-one order at the bottom. The
position of the detector is indicated on the right hand side.
Notice that the image can be much larger than the detector, and
depending on the incoming ray angle, certain orders will fall off
the image.
|
|
|
|
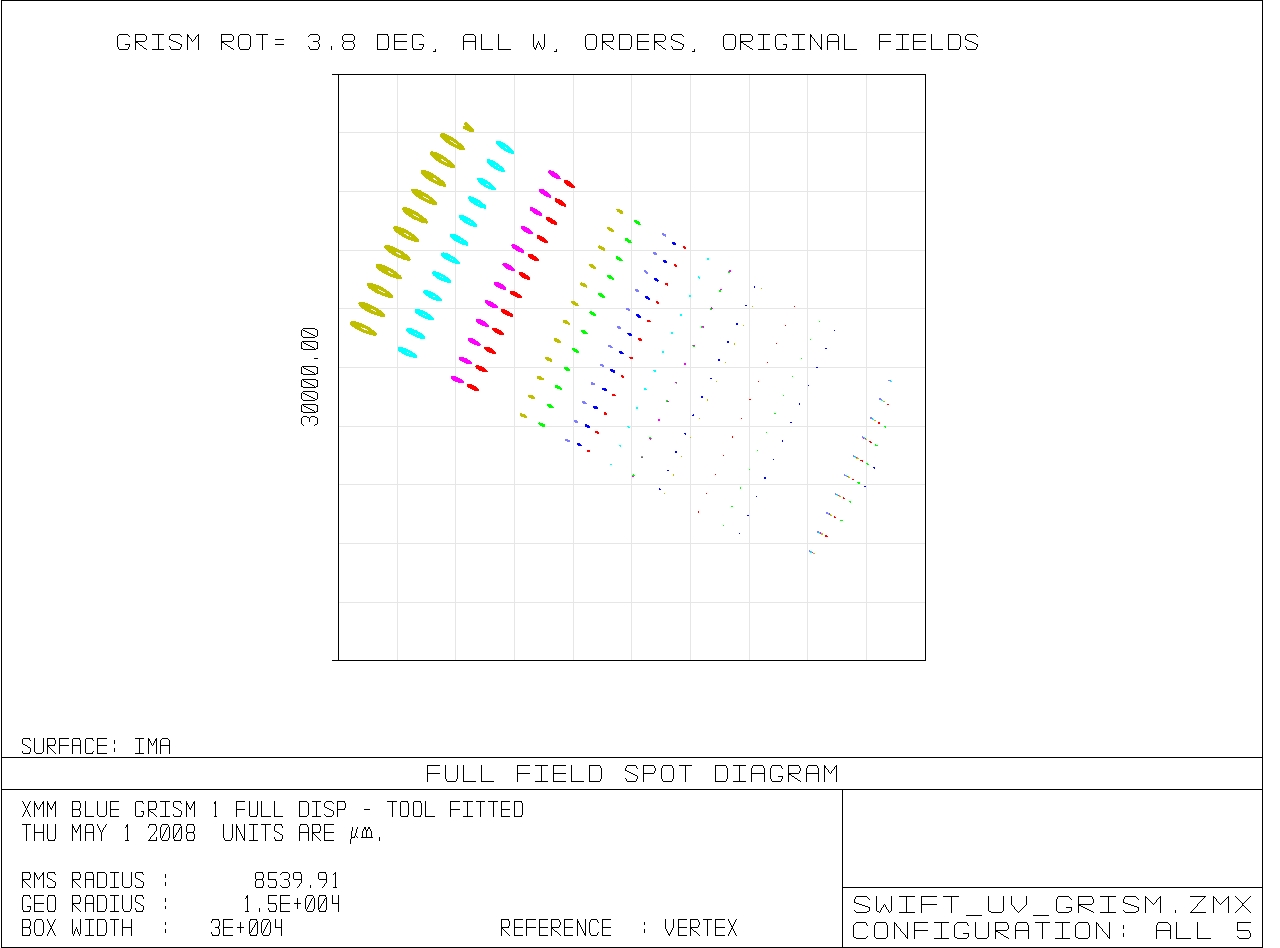
Figure 2: The spot diagrams have been calculated for
orders -1,0,1,2, and 3 at 12 field positions and 7
wavelengths. To the left the third order shows very elongated PSF
with a dip in the center. Also, the direction of the elongation is
not completely parallel to the dispersion plane. The actual linear
size of the detector is about 19 mm, so the detector would cover
only the central part of this image which is 30 mm on each side.
|
The Zemax model for a source on the optical axis
The orginal Zemax UVOT model was used for the design of the OM and
UVOT, but no adjustments were made based on the actual instrument
past the design phase. Although the instrument was build within
specifications, the direction of the dispersion plane as measured
from observations at the boresight is different from the model.
Observations with the UVOT grisms are regularly done in two
filterwheel positions, the socalled 'Nominal' position is where the
grism is centered on the optical axis, while in the socalled
'Clocked' position the filter wheel has been rotated by 40 steps, and
only part of the grism is in the optical path. The measured
angles of the dispersion in the first order around 300nm
differs in these positions by the filterwheel rotation over the 40
steps. Therefore we have two measurements of the angle which give an
initial estimate of the angle of the dispersion plane of the grism,
relative to the model of 3.8 ± 0.2 degrees.
The
interpretation of the cause of this extra angle is important, since
that will tell us which element in the Zemax model needs adjustment.
Based on the design of the grism, the mounting of the detector and
the filterwheel, and considering the knowledge from observations with
the lenticular filters, the most likely cause is a slight rotation
caused when mounting the grism within the filterwheel. This
slightly inaccurate alignment of the dispersion direction of the
grism is considered to be within expectations.
Therefore the
angle of the dispersion plane of the grism with respect to the
filterwheel has been adjusted by the required 3.8 degrees in the
model calculations used.
For this study, the wavelengths in
Table 1 were used.
Table 1: Zemax results
for the ray on the optical axis.
|
|
zero order
|
first order
|
second order
|
|
wavelength
(nm)
|
X (pix)
|
Y (pix)
|
X (pix)
|
Y (pix)
|
X (pix)
|
Y (pix)
|
|
190
|
1604.34
|
616.94
|
1178.81
|
850.87
|
764.59
|
1078.59
|
|
214
|
1570.88
|
635.33
|
1093.26
|
897.91
|
626.85
|
1154.32
|
|
260
|
1537.15
|
653.88
|
959.25
|
971.57
|
390.86
|
1284.06
|
|
330
|
1513.97
|
666.62
|
783.29
|
1068.3
|
52.87
|
1469.87
|
|
400
|
1502.82
|
672.75
|
619.07
|
1158.60
|
off
|
off
|
|
450
|
1497.97
|
675.42
|
504.46
|
1221.60
|
off
|
off
|
|
550
|
1491.94
|
678.73
|
276.99
|
1346.66
|
off
|
off
|
The calculated second order point at 190nm nearly overlaps
with the first order point around 330nm (see yellow highlights).
Longwards of that point, the second order spectrum can cause
confusion with the first order spectrum. In practice, the width of
the observed first order spectrum is about 15 pixels, so the first
and second order overlap here. Notice that the calculated first order
point at 260 nm (highlighted in blue) is close to the centre
(1023.5,1023.5) of the detector, but does not fall right on top of
it. This suggests that a shift to the model may be needed to bring it
into accord with boresight observations as discussed below.
A few words are needed to explain the coordinate system
used. The boresight in the lenticular filters is specified in
the RAW coordinate system, as specified in the UVOT CALDB
Teldef files. Since the boresight is equivalent to the point
where the optical axis of the system crosses the image plane, I have
choosen to adopt a similar coordinate system for the current study.
The actual image coordinates produced by the Zemax model are in
detector coordinates which are measured in mm from the
centre of the detector. For the table I have converted them to pixels
using the scale factor of 0.009075 mm/pixel (See the Teldef
Document). In the following, the Zemax model calculations
will therefore be compared to observations in detector
coordinates, but converted to the same pixel coordinate system as
RAW. The mapping from RAW to DETector
coordinates makes the correction for distortions due to the fiber
taper in the detector. The distortion correction is not included in
the Zemax model. Near the centre of the detector, where the
distortion correction is small, results from zemax and the
observations can be compared with ease to the filter boresight data
in the raw coordinate system.
As can be seen, the zero order
position falls far from the detector centre. This is the reason that
identification of the zero order with the boresight of the grisms can
lead to a boresight point for the grisms that is far from the ones
for the lenticular filters. However, the reference wavelength
for the design of the UV grism was 260 nm in the first
order, so that should be the appropriate wavelength and order to
compare with.
Observations of Wolf-Rayet wavelength calibrators near the
boresight
Observations were made with the UV grism of two broad-line
emission stars, WR52 and WR86, attempting to centre the stars at the
boresight. The observations were directly followed by
observations in a lenticular filter during the same AT sequence.
Since during an AT sequence the position is held steady, only minor
drifts, less than 2" are expected between the image taken in the
lenticular filter and that in the grism. Images in the uvw1 filter
taken right before these showed substantial offsets, though. Details
of the observation sequences are given in Table 2.
Table 2
|
Source
|
UVOT
|
image
|
Date & time(UT)
|
filter
|
distance to boresight
|
|
ID
|
Obs ID
|
|
|
|
X (pix)
|
Y (pix)
|
|
WR52
|
56950007
|
w1231394014I
|
2008-05-02T04:06:53
|
uvw1
|
4.7
|
-4.9
|
|
WR52
|
56950007
|
gu231393684I
|
2008-05-02T04:01:23
|
gu
|
|
|
|
WR86
|
57000005
|
w1231383514
|
2008-05-02T01:11:53
|
uvw1
|
16.6
|
-10.3
|
|
WR86
|
57000005
|
gu231383183I
|
2008-05-02T01:06:22
|
gu
|
|
|
|
WR52
|
56950007
|
w1231399744I
|
2008-05-02T05:42:23
|
uvw1
|
17.9,
|
-12.6
|
|
WR52
|
56950007
|
gu231399443I
|
2008-05-02T05:37:22
|
gu
|
|
|
|
WR86
|
57000005
|
w1231389214I
|
2008-05-02T02:46:53
|
uvw1
|
21.9
|
-3.7
|
|
WR86
|
57000005
|
gu231388883I
|
2008-05-02T02:41:22
|
gu
|
|
|
Earlier spectra of both objects were published. Shortward of
about 330nm data from the IUE INES archive were used;
for WR52 swp39140,lwp18178,and lwr10488, for WR86 swp25312,and
lwp05417, which provides spectra that are absolutely calibrated.
Longward of 345nm the atlas by Torres-Dodgen and Massey (1988;
ADC catalog 3143) provides ground-based observations, which are
rectified. Since we are only concerned with the wavelength scale, the
spectra were matched up by multiplying the data with an arbitrary
factor in the flux scale. These reference spectra are shown in
Figure 3.
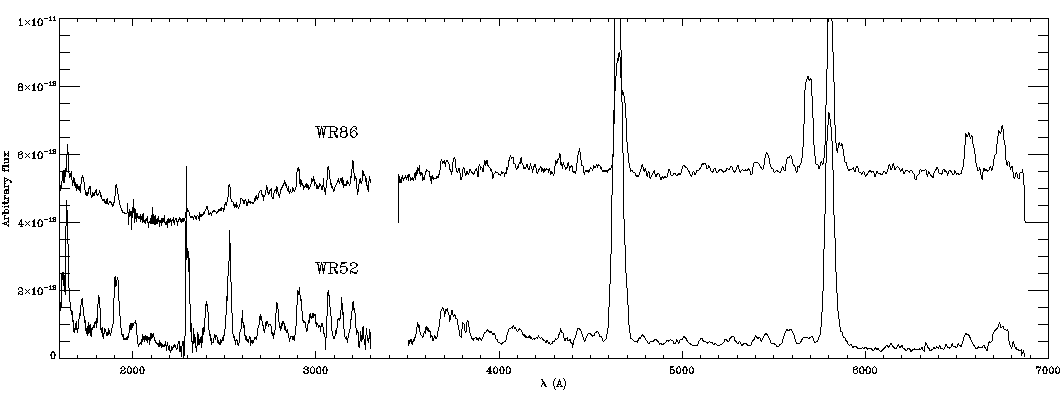
Figure
3. Reference spectra used.
Spectral line identifications in the WR stars
The observed UVOT UV-grism spectra were extracted using the Ftools
program uvotimgrism and Wayne Landsmans grismspec
IDL procedure, to further process the uvotimgrism output in
IDL. The spectrum of WR 52, and both spectra of WR86, are shown
in Figure 5. The dominant spectral lines for these stars are
readily identified in their spectra and are consistent with
their spectral classification as early WC stars. The
list of well-identified spectral lines is listed in Table 3. The
identified lines need to be used due to possible confusion with
second order spectral lines when deriving the dispersion
relation.
Table 3
|
Wavelength
|
Identification
|
WR52
|
WR86
|
|
1816
|
unid. (Si II ?)
|
present
|
|
|
1909
|
C III
|
present
|
present
|
|
2010
|
C III
|
present
|
|
|
2297
|
C III
|
present
|
present
|
|
2405
|
C IV
|
present
|
present
|
|
2530
|
C IV (3)
|
present
|
present
|
|
2595
|
C IV
|
present
|
|
|
2699
|
C III
|
present
|
present
|
|
2787
|
O V (3), C III(3)
|
present
|
|
|
2906
|
C IV
|
present
|
present
|
|
3070
|
O IV
|
present
|
present
|
|
3130
|
O III
|
present
|
present
|
|
3203
|
He II, O IV, Si III
|
present
|
present
|
|
3265
|
O IV
|
|
present
|
|
3409
|
O IV
|
present
|
present
|
|
3762
|
O IV
|
|
present
|
|
4069
|
C III
|
present
|
present
|
|
4442
|
C IV
|
|
present
|
|
4649
|
C III
|
present
|
present
|
|
5696
|
C III (flat top)
|
|
present
|
|
5801
|
C IV
|
present
|
|
Determination of the dispersion in the spectra and unscaled Zemax
results
The pixel start points of the two spectra of each star were
shifted to align them. Each pair of spectra then matches very well,
with the exeption of some extra features in one or the other spectrum
that can be attributed to zero order contaminations from other stars
in the field, see Fig. 5. Since the spectral features in the two
exposures all overlap closely, the best spectrum was selected for the
fit. A gausian was fit to the spectral lines in the observed spectra
using the IDL procedure XCFIT (written by S.V.H. Haugan, 1997).
The dispersion relations and their inverse that were derived for the
observed spectra can be found in Table 4, with D the dispersion in
pixels and λ the wavelength in Angstrom The anchor point
for the wavelength scale should be considered to be quite arbitrary.
Table 4
|
#
|
Spectrum
|
formula
|
N
|
a0
|
a1
|
a2
|
a3
|
a4
|
|
1
|
WR52
|
λ = ΣN an Dn
|
3
|
1358.2
|
0.41046
|
0.00293119
|
-8.2427e-07
|
|
|
2
|
WR86
|
λ = ΣN an Dn
|
4
|
1732.3
|
-1.8233
|
0.00800797
|
-5.4632e-06
|
1.4792e-09
|
|
3
|
WR52
|
D = ΣN an λn
|
3
|
-634.4
|
0.70315
|
-0.00010255
|
7.74121e-09
|
|
|
4
|
WR86
|
D = ΣN an λn
|
4
|
-1099.4
|
1.30413
|
-0.00038863
|
6.51949e-08
|
-4.1243e-12
|
Determination of the Zemax pixel scale
Using the inverse of the dispersion relation, a fit of pixel scale
against wavelength is also given. Using the inverse fit, the pixel
coordinates (with arbitrary anchor point) can be determined for the
wavelengths used in the zemax model. For the zemax
calculations, the pixel distances between neighboring points was
added to derive the pixel distance to the first point. A linear
and quadratic fit were made between the zemax pixel distances and the
observed pixel coordinates. This shows that the relation is nearly
linear, and a scale factor to convert the zemax pixel scale to the
observed pixel scale is found for both stars. These are listed
in table 5. The weighted average pixel scale factor for Zemax pixels
is 0.945 ± 0.003.
Table 5: DET pixel
to zemax pixel
|
Fitted spectra
|
Scale factor
|
|
WR52
|
0.944 ± 0.003
|
|
WR86
|
0.948 ± 0.005
|
The zemax pixel positions used from hereon will have been
scaled using the factor as determined here. The source of the factor
is the unknown scaling within the detector (which was not included in
the Zemax optical model) due to the fiber taper etc. .
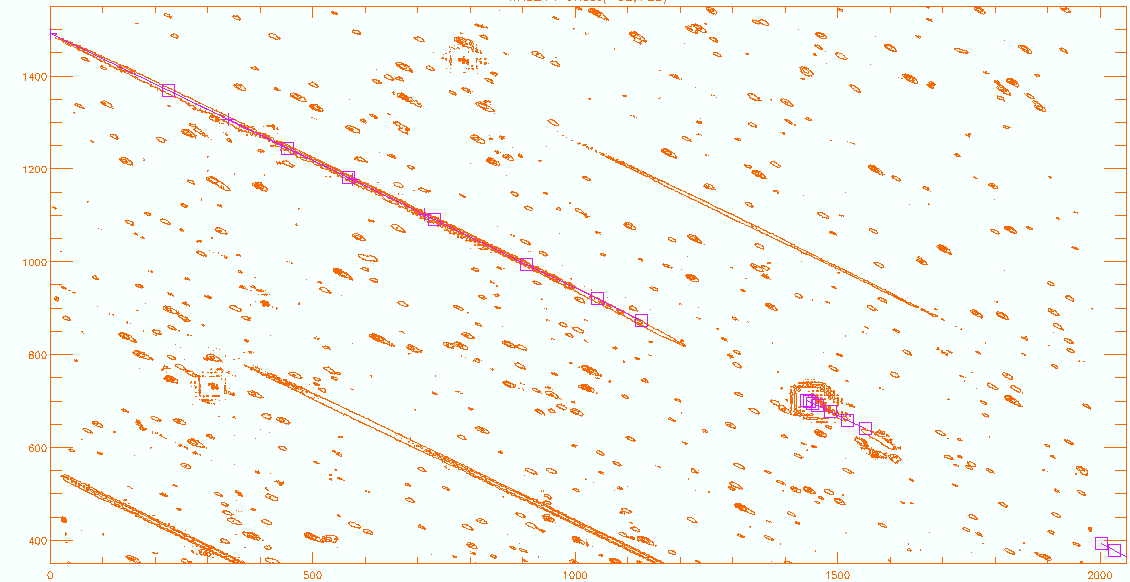
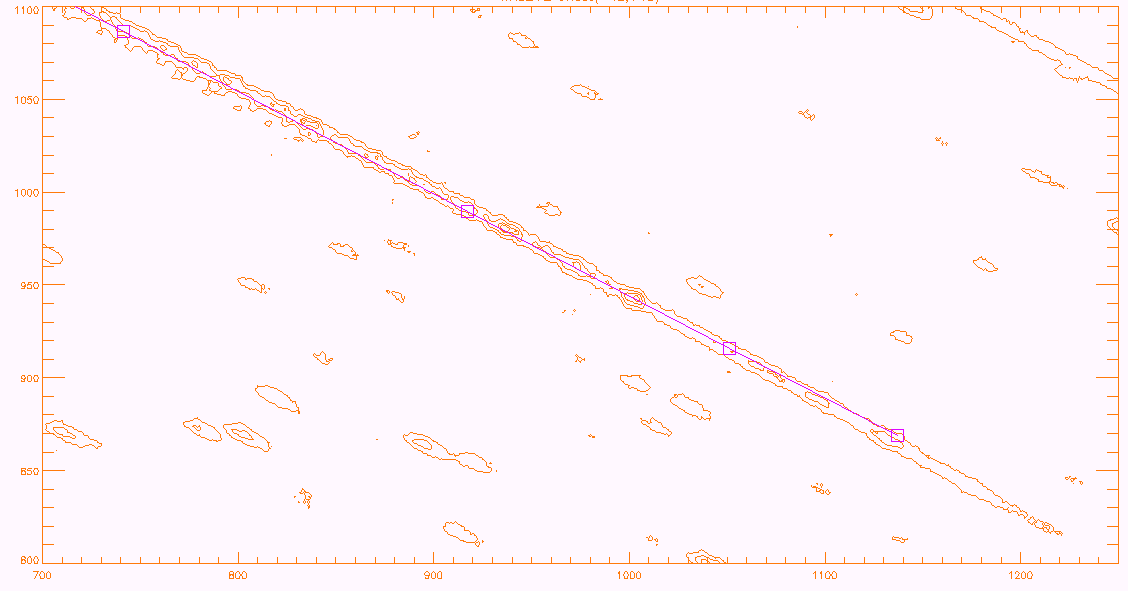
Matching the Zemax spectral points
Using a contour plot of each of the four UV grism image, the zemax
data for the optical axis were shifted to match the data at 260 nm.
In order to do that, the location of the 260nm feature in the
observed spectrum had to be located, which in the case of WR86 proved
to be problematic. The accuracy of the fits is best in WR52, and
limited by the match by eye, and is at least 5 pixels in x, 3 in Y.
For WR86, the uncertainty is larger. The fits of the zemax
calculations to the observed spectra are shown in Figure 4. It
can be seen, that the zemax model calculations overlie the zeroth,
first and second orders correctly. The square symbols were used for
the zero and first order, crosses for the second order. The web
page has a link to the full image.
|
|
|
|
Figure 4a: WR52 [gu231393684I] contour map with zemax points
|
Figure 4b: WR52 [gu231399443I] detail around 260nm in first
order
|
|

|

|
|
Figure 4c: WR52 [gu231399443I] contour map with zemax
point
|
Figure 4d: WR86 [gu231388883I] with zemax points
|
Table 6
|
#
|
star
|
pixel offset on
grism det image to
match
260nm
|
|
1
|
WR52
|
-25
|
24
|
|
2
|
WR52
|
-15
|
19
|
|
3
|
WR86
|
-20
|
23
|
|
4
|
WR86
|
-13
|
31
|
Currently, the data for the offsets are not good enough to
derive a consistent picture based on a scale factor and an offset.
This may be due to a remaining spacecraft drift during the
observations, but mostly, because the matching needs to be
improved using a different technique. This will be reported on in a
future report.
The offset is about (ΔX,ΔY)=(-20,20)
from the zemax model positions, while the average source offsets are
about (ΔX,ΔY)=(10,-10) from the UVOT borepoint
based on the uvw1 positions. So, a total shift of about
(ΔX,ΔY)=(-30,30) may need to be applied to the
zemax model positions to align them with the observations.
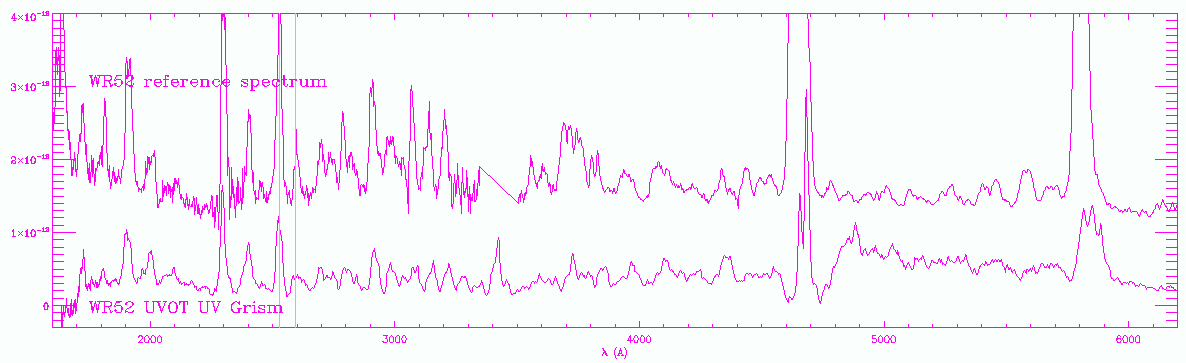
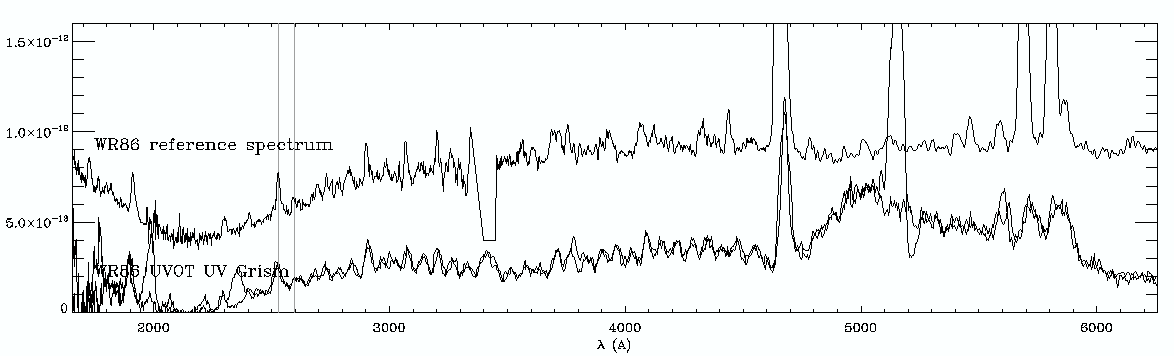
In
Fig. 5 the zemax dispersion relation for the first order has been
used to apply a wavelength scale to the observations. The wavelength
scale was anchored to the 260nm feature, since we are still working
out a more precise shift that is needed, as discussed above. The
reference spectra were shifted upward in flux, and show that
the overal wavelength scale is good. In the WR86 spectrum, the two
observations have been plotted on top of each other to show
repeatability. Please note that the fluxes are uncalibrated.
|
|
|
Figure 6a: Comparison of the WR52 observed spectrum
with zemax wavelength scale to the reference spectrum. Vertical
lines are at the wavelengths of two lines, 2530, and 2595 Å
|
|
|
|
Figure 6b: Comparision of the two WR86 observed
spectra to the reference spectrum. Vertical lines are at the
wavelengths of two lines, 2530, and 2595 Å
|
Check of the dispersion plane angle
The dispersion plane angle correction of 3.8 ±
0.2 degrees was based on the values in the UVOT software
documentation. Since we have observations of WR52 and WR86 in both
clocked and nominal mode, both taken near the boresight, the
angles of the first order on the detector image were measured in the
region around 260nm using DS9 to align a vector over
the peaks of the spectral features. An average angle of the
spectrum was measured for the clocked position of 144.28 ±
0.01 deg. (2 measurements), and in the nominal position the angle was
151.00 ± 0.06 deg. (4 measurements). The filterwheel
rotation between the clocked and nominal position is 6.545 deg. and
the rotation angle of the filterwheel at the nominal position is
155.00 deg. That leads to a difference with the dispersion plane
derived from the nominal position of 4.00 ± 0.06 deg. and
the clocked position gives 4.18 ± 0.06 deg., where the
error in the clocked position was increased to the one found in the
nominal position, since not enough points were used to give a
reliable error. The average value for the dispersion plane
rotation is thus 4.1 ± 0.1 deg. Since the angle of
the first order varies with position on the detector, that does not
invalidate the CALDB document, but the values found here give tighter
values for observations at the borepoint around 260nm in the first
order. The slight discrepancy with the angle used for the analysis
above will not impact any quantitative results.
Summary of results
A scale factor for the zemax model
pixels of 0.945 ± 0.003 was determined.
After shifting the zemax model
data, the zemax points overlay the observed spectrum positions well
in all visible orders.
The predicted positions for the
first order spectrum line up well with the observed spectrum, which
shows that the zemax dispersion relation is right.
No objection has been found for
using the zemax model for predicting the observed grism image.
A better value for the angle of the dispersion plane has been
determined of 4.1 ± 0.1 deg..