XMM Users' Handbook

   
Components of the RGS LSF

The RGS angular (or wavelength-) response to monochromatic radiation - and thus its LSF - consists of two distinct physical components. The core of the profile is determined by geometrical optics: the telescope angular response, the grating figures, the grating-to-grating alignment, and the focusing of the telescope. This core can be calculated reliably with a raytrace code, based on an explicit model for the various components of the RGS. The parameters of this model have been calibrated in separate tests at sub-assembly level (telescope, RGA, individual gratings), and the resulting model has been validated in end-to-end tests of both spectrometers at the Panter X-ray testing facility of the Max Planck Institut für extraterrestrische Physik.

Microroughness on the gratings causes scattering of light, the amplitude and angular distribution of which scale completely differently with wavelength and dispersion angle (or spectral order) from the core shape. A theoretical model for the redistribution of light due to scattering was developed, based on first order perturbation theory for scalar diffraction. The free parameters of this model, the rms amplitude and correlation length of the surface fluctuations, were calibrated on a large subset of the gratings and the resulting scattering redistribution kernel was verified in the end-to-end tests at Panter.

  

Figure 53: Response of RGS-1 to Mg K$\alpha$ radiation (E = 1.25 keV; $\lambda \ = 9.89\ \AA$), in orders m=-1,-2, respectively, as measured at Panter. The excess seen on the right side of the profile is due to the presence of fainter, slightly higher energy lines in the emission spectrum of the calibration source (which was also included in the input to the simulations). The second order profile shows that the outer wings of the scattering distribution are currently underpredicted. For reference, 1 mm in the focal plane equals 0.104 Å at Mg K$\alpha$, m = -1, and 0.0665 Å at Mg K$\alpha$, m = -2.

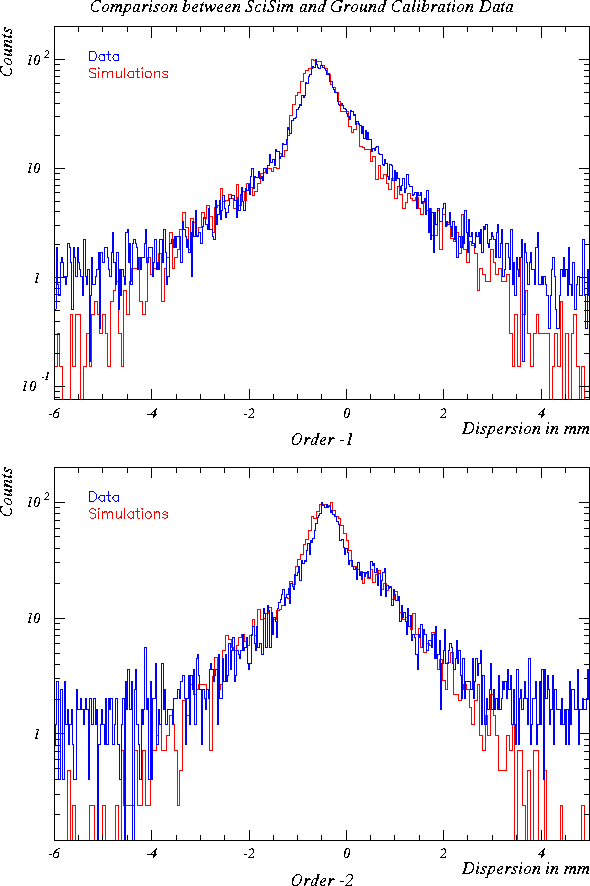
The characteristic two-component shape of the resulting LSF (response integrated over the cross-dispersion direction) can be seen in Fig. 53, which shows the response of RGS-1 to Mg K$\alpha$ radiation at 1.25 keV energy in the -1. and -2. spectral order, as measured at Panter, on a logarithmic scale so as to enhance the visibility of the line wings. Overlaid on the data are simulations calculated with the current best model for the instrument. As is clear from these figures, the LSF can not adequately be represented by a single simple profile function (e.g., Gauss or Lorentzian) at all wavelengths. Therefore, to characterize the resolving power of the RGS, two separate measures are shown above, one based on the HEW of the LSF, one based on the FWHM (Figs. 48 and 49).

At low energies (long wavelengths), scattering is unimportant, and the LSF is dominated by the nearly-Gaussian core of the profile. The resolving power therefore asymptotically approaches approximately

$${\cal R} \equiv\ \lambda/\Delta\lambda\ \sim\ {\rm constant}\times\lambda$$ (1)

since $\Delta\lambda$ for the core is only a weak function of $\lambda$. At short wavelengths, scattering is relatively more important, and the resolving power curves decline faster than proportional to $\lambda$. Final modeling of the scattering behaviour in this regime is still in the process of refinement, and the precise shape of the resolving power curves for energies above ca. 1.5 keV ( $\lambda \leq\ 8$ Å) may therefore change somewhat with improved modeling.